Power is the rate of doing work. The letter symbol for power is P. The watt (W) is the Si unit of power. One watt is equal to one joule per second: 1 W = 1 J/s
Equation 1 shows the relationship between power and work:
\[\begin{matrix} P=\frac{W}{t} & {} & \left( 1 \right) \\\end{matrix}\]
Where P is power in watts, W is work in joules, and t is a time in seconds.
When dealing with work and power, keep in mind that joules are a measure of energy while watts are a measure of the rate of transferring energy.
We can use the equations for potential difference and current to relate these quantities to power in a circuit.
Since,
$V=\frac{W}{Q}$
So,
$W=VQ$
Similarly,
\[I=\frac{Q}{t}\]
So, Substituting for W and t in Equation 1 gives
\[\begin{matrix} P=\frac{W}{t}=\frac{VQ}{{}^{Q}/{}_{I}}=V\times I & {} & \left( 2 \right) \\\end{matrix}\]
Where P is power in watts, V is a voltage drop in volts, and I is current in amperes.
We can also substitute V = IR (voltage drop) into Equation 2 to get
$\begin{matrix} P=V\times I=IR\times I={{I}^{2}}R & {} & \left( 3 \right) \\\end{matrix}$
Where P is power in watts, I is current through the resistance in amperes, and R is resistance in ohms.
Similarly, substituting I = V/ R into Equation 2 gives
$\begin{matrix} P=V\times I=\frac{{{V}^{2}}}{R} & {} & \left( 4 \right) \\\end{matrix}$
Where P is power in watts, V is a voltage drop across the resistance in volts, and R is resistance in ohm.
Electric Power Calculation Example
A lamp draws a current of 2.00 A when connected to a 120-V source. How much power is going to the lamp?
Solution
$P=E\times I=120V\times 2A=240W$
When designing circuits, we need to specify the power rating of a resistor as well as its resistance. Since a resistor converts all power it consumes into heat, the power rating is the rate at which the resistor can dissipate heat without damage.
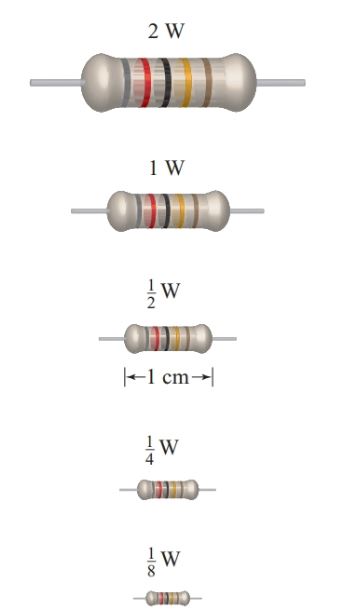
Heat dissipation depends on the surface area of the resistor and therefore on its physical size. Standard carbon-composition resistors are manufactured in sizes ranging from 1/8 W to 2 W, as shown in Figure 1.
Figure 1 Approximate sizes of carbon-composition resistors
Resistor Power Rating Example
A 10-kV resistor is connected into a circuit where the current through it is 50 mA. What is the minimum power rating required for this resistor?
Solution
$P={{I}^{2}}R={{\left( 50mA \right)}^{2}}\times 10k\Omega =25W$
The resistor should be rated for at least 25 W.
Voltage Calculation Example
What is the highest voltage that can be applied to a 3.3-kV, 2.0-W resistor without exceeding its heat-dissipating capability?
Solution
Since,
\[P=\frac{{{V}^{2}}}{R}\]
And,
$V=E=\sqrt{PR}=\sqrt{2W\times 3.3k\Omega }=81V$
Efficiency
Almost all equipment converts some of its input energy into a form that does not produce useful work. This wasted energy is usually in the form of heat.
The wasted energy increases the cost of making the equipment as well as the cost of running it since the equipment has to be designed to dissipate the wasted energy safely.
The efficiency of a device indicates how much of the input energy, Win, the device converts into useful work, Wout.
Efficiency is the ratio of useful output energy to total input energy. The letter symbol for efficiency is the Greek letter η (eta).
\[\begin{matrix} \eta =\frac{{{W}_{out}}}{{{W}_{in}}} & {} & \left( 5 \right) \\\end{matrix}\]
We usually express efficiency as a percentage.
Efficiency Calculation Example
What is the efficiency of an electric hoist if its motor uses 60 KJ to raise a 300-kg mass through 18 m?
Solution
\[{{W}_{out}}=300kg\times 9.8{}^{m}/{}_{{{s}^{2}}}\times 18m=52.9kJ\]
\[\eta =\frac{{{W}_{out}}}{{{W}_{in}}}=\frac{52.9kJ}{60kJ}\times 100=88%\]
Since,
\[P=\frac{W}{t}\]
So,
$W=Pt$
Substituting for Wout and Win in Equation 5 gives
\[\eta =\frac{{{W}_{out}}}{{{W}_{in}}}=\frac{{{P}_{out}}\times t}{{{P}_{in}}\times t}\]
So,
\[\begin{matrix} \eta =\frac{{{P}_{out}}}{{{P}_{in}}} & {} & \left( 6 \right) \\\end{matrix}\]
For electric motors, Pout is mechanical power output, and Pin is electric power input. All types of power can be measured in watts. However, in North America, the mechanical power output of motors is often expressed in terms of horsepower (hp), a unit invented by James Watt:
\[\begin{matrix} 1\text{ }hp=746\text{ }W & {} & \left( 7 \right) \\\end{matrix}\]
Input Power Calculation Example
Find the input power for an electric motor that has an output of 24 hp and an efficiency of 85%.
Solution
$\begin{align} & {{P}_{out}}=24hp=24hp\times \frac{746W}{1hp}=17.9kW \\ & {{P}_{in}}=\frac{{{P}_{out}}}{\eta }=\frac{17.9kW}{0.85}=21kW \\\end{align}$
The Kilowatt Hour
A joule is a relatively small quantity of energy. A typical home uses millions of joules of electrical energy each day. Since power × time = energy, we could use the product of any unit of power with any unit of time as a measure of energy.
In fact, a joule is equal to a watt-second. If we measure power in kilowatts and time in hours, we can use kilowatt hours (kWh) as a unit for energy:
$W=Pt$
Where W is work or energy in kilowatt hours, P is power in kilowatts, and t is a time in hours.
Since
1 kW = 1000 W and 1 h = 3600 s,
$\begin{matrix} 1kWh=1000W\times 3600s=3.6\times {{10}^{6}}J=3.6MJ & {} & \left( 8 \right) \\\end{matrix}$
Many North American electric utilities measure their customers’ energy consumption in kilowatt hours.
Most meters that record electric energy consumption are a form of a motor with an aluminum disk that rotates at a speed directly proportional to both the applied voltage and the current.
Since P = EI, the speed of the disk is proportional to the power used at any given moment, and the number of rotations indicates the energy consumed (power times time).
Example 6
At 7¢ per kilowatt-hour, how much will it cost to leave a 60-W lamp burning for five days?
Solution
$\begin{align} & W=Pt=60W\times 24h\times 5=7200Wh=7.2kWh \\ & Cost=7.2kWh\times \frac{7c}{kWh}=50.4c \\\end{align}$