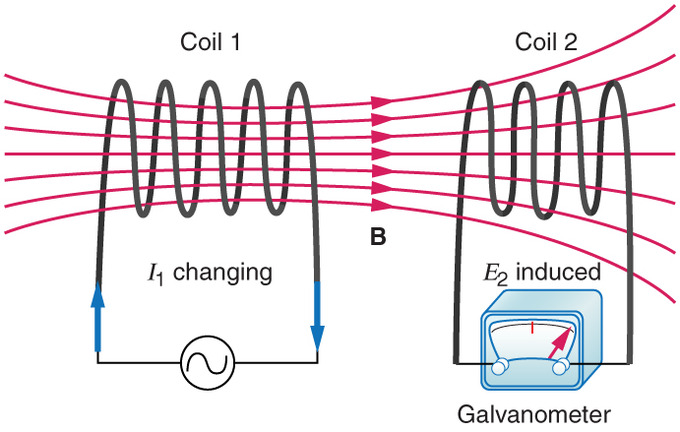
Definition: When two coils are within magnetic reach of each other so that the flux lines of one coil link with, or cut across the other coil, they have mutual inductance.
If the coils are close to each other, many magnetic lines of flux from the first coil will link with the second coil. On the other hand, if the coils are a distance apart, there might be very little linkage.
Figure: Mutual Induction
The mutual inductance of two coils can be increased if a common iron core is used for both coils.
The degree to which the lines of force of one coil link with the windings of the second coil is called coupling.
If all lines of one cut across all the turns of the other, we have what is called unity coupling. Any number of percentages of coupling can exist due to the mechanical position of the coils. The amount of mutual inductance can be found using the formula:
${{L}_{M}}=k\sqrt{{{L}_{1}}\times {{L}_{2}}}$
Where LM is the mutual inductance in henrys, k is the coefficient or percentage of coupling, and L1 and L2 are the inductances of the respective coils.
Mutual inductance must be considered when two or more inductors are connected in series or parallel in a circuit.
The Relationship in Series and Parallel Inductance
When coils are joined in series, the total inductance is:
${{L}_{T}}={{L}_{1}}+{{L}_{2}}+{{L}_{3}}+\cdots +{{L}_{N}}$
Notice that the individual inductances add together like series resistors. However, when there is mutual inductance the formula becomes:
${{L}_{T}}={{L}_{1}}+{{L}_{2}}\pm 2{{L}_{M}}$
The plus or minus sign (±) before the 2LM means that the mutual inductance value might be added or subtracted depending on whether the magnetic fields are aiding or opposing each other. The plus (+) should be used when the coils aid each other. The minus (–) should be used when the coils oppose each other.
When inductors are connected in parallel without mutual inductance, the total inductance can be calculated using the formula:
\[\frac{1}{{{L}_{T}}}=\frac{1}{{{L}_{1}}}+\frac{1}{{{L}_{2}}}+\frac{1}{{{L}_{3}}}+\cdots +\frac{1}{{{L}_{N}}}\]
The formula is structured the same as the parallel resistance formula.
When only two inductors are being added in parallel, the product over the sum formula can be used.
\[{{L}_{T}}=\frac{{{L}_{1}}\times {{L}_{2}}}{{{L}_{1}}+{{L}_{2}}}\]
Notice that here again, inductors in parallel add like resistors in parallel.
Mutual inductance is widely used in electricity and electronics. A skilled technician must have a complete understanding of the characteristics of circuits containing these components.