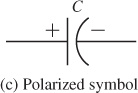A resistor presents a fixed value of resistance (opposition to current) that is independent of the type of voltage (dc or ac) applied to it. Capacitors and inductors are two types of electrical components classified as reactive, which means that their opposition to current depends on the type of voltage and the frequency of the applied ac voltage. The opposition to current that a capacitor or inductor presents in a circuit is called reactance. When reactance and resistance are both present in a circuit, the combination is called impedance.
Capacitors
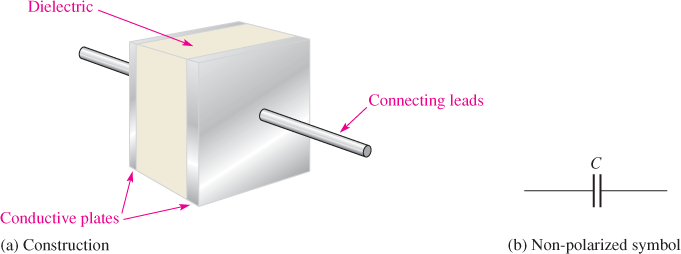
A capacitor is an electrical device that stores energy in the form of an electric field established by an electrical charge. In its most basic form, the capacitor is constructed of two conductive plates placed physically in parallel and separated by an insulating material called the dielectric. Connecting leads are attached to the parallel plates. The basic capacitor structure is shown in Figure 1(a). The schematic symbol for a non-polarized capacitor is shown in Figure 1(b); the schematic symbol for a polarized capacitor is shown in Figure 1(c). A polarized capacitor must be put in the circuit in the correct direction. Capacitors are available in fixed or variable types.
Figure 1: Basic Capacitor and its Symbols
Capacitance Formula
The amount of charge that a capacitor can store per unit of the voltage across its plates is its capacitance (C). The more charge per unit of voltage that a capacitor can store, the greater its capacitance, as expressed by the following formula:
\[C=Q/V\]
Where
C is capacitance in farads
Q is charge in coulombs
V is voltage in volts
Capacitance depends on the area of the plates and the distance between them. Some typical capacitors are shown in Figure 2.
Unit of Capacitance
The farad (F) is the unit of capacitance. One farad is the amount of capacitance when one coulomb (C) of charge is stored with one volt across the plates. Smaller values of capacitance are expressed in microfarads (μF) or in Picofarads (pF). A microfarad is one-millionth of a farad; a Pico farad is one-trillionth of a farad. Capacitors are available from very small to very large, both in capacitance and physical size. Generally, very large capacitors (>1 μF) are polarized.
 |
 |
 |
 |
Figure 2: Examples of Capacitors
How a Capacitor Stores Energy
Energy is stored in the form of an electric field that is established by the opposite charges stored on the two plates. The electric field is concentrated in the dielectric of the capacitor. When a capacitor is connected across a voltage source, the plates acquire a charge that is positive on one plate and negative on the other. This creates the electric field between the plates, which stores energy. The energy stored is proportional to the capacitance and the square of the voltage across the plates, as expressed by the following formula:
\[W=\frac{1}{2}C{{V}^{2}}\]
When the capacitance is in farads and voltage is in volts, energy is in joules.
Applications
Capacitors are used in a wide variety of applications. They can be used to block direct current and pass or reject certain ac signals with certain frequencies. They are used in ac to dc converters that change an ac input to a dc output. Large capacitors are also used to store energy in solar power applications and other renewable resource applications to provide power when the resource is not available; however, cost remains a major factor in using capacitors for energy storage.
Figure 3: Coil of Insulated Wire Forms an Inductor. When there is current through the coil of wire, a three-dimensional magnetic field is created. With the fingers of the left hand wrapped toward electron flow, the thumb will point to the North Pole.
Inductors
Current through a wire creates a magnetic field around the wire. An inductor is basically a length of insulated wire formed into a coil. Current through the coil creates a much stronger magnetic field than the magnetic field for a straight wire. Figure 3 illustrates an inductor with current through it; Figure 4 shows some typical inductors.
Figure 4: Several Typical Inductors
Inductance
Inductance is the ability of a wire conductor to oppose a change in current. Inductance is a property of all conductors, but it has only a tiny effect in straight wire conductors. It is much more pronounced in coils because of the enhanced magnetic field surrounding a coil. In fact, coils are usually referred to as inductors because they are selected for their inductive properties. Motors, generators, and transformers are all devices that depend on coils to operate. These topics are covered later in this text.
Unit of Inductance
The unit of inductance is the Henry (H).
The inductance of a coil is one Henry when the current through the coil changing at one ampere per second induces one volt across the coil.
Smaller values of inductance are expressed in milli-henries (mH) or in micro-henries (μH).
When current starts in an inductor because of an applied voltage, an electromagnetic field expands outward from the coil. This field stores energy. As the field expands, a voltage is induced across the coil and acts in opposition to the original voltage. As a result, it opposes a change in the original current. Once the current has reached a steady value, the electromagnetic field no longer expands, and no voltage is induced in the coil. This fundamental action is defined by Lenz’s law, which states:
When the current through a coil changes, an induced voltage is created across the coil in a direction that always opposes the change in the current.
You have seen that opposition to current can be of resistance, capacitance, or inductance. For capacitors and inductors, the opposition is called reactance. The combination of reactance and resistance is called impedance.
Transformers
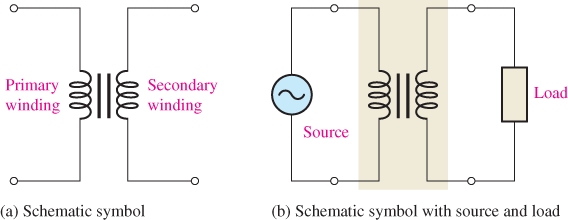
A transformer is a device formed by two or more coils (commonly called windings) around a common core that are magnetically coupled to each other and provide for the transfer of ac power electromagnetically from one winding to the other. Most power transformers are used to change ac from one ac voltage to another. A transformer will not transfer dc from one winding to the other. A schematic symbol is shown in Figure 5. One coil is called the primary winding, and the other coil is called the secondary winding. An ac source voltage is applied to the primary winding, and a load is connected to the secondary winding, as shown in Figure 5(b).
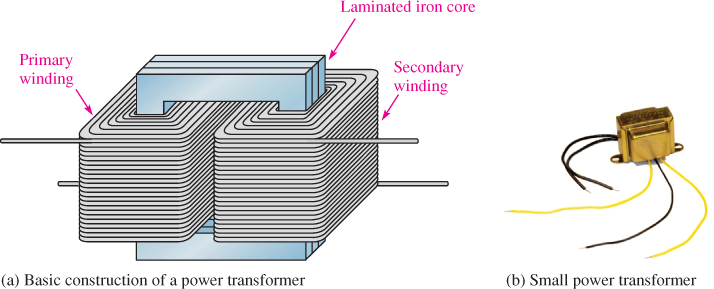
Several power transformers are illustrated in Figure 6; all are power types that use an iron core but are very different in size. The basic construction of a power transformer is shown in Figure 6(a). Figure 6(b) shows a small power transformer such as you might find in an electronic controller or other electronic devices. Three utility pole transformers connected to a commercial building are shown in Figure 6(c), and very large transformers at a power plant are shown in Figure 6(d).
Figure 5: Transformer Schematic
Figure 6: Typical Power Transformers. Power transformers range in size from very small transformers to huge power plant transformers.
Transformer Action
Recall that a changing magnetic field can produce an induced voltage, which is the basic idea behind transformer action. A changing current on the primary side produces an electromagnetic field in the core, which follows the changing current. This changing electromagnetic field induces a voltage across the secondary coil. Keep in mind that a transformer can work only with an ac input because it is necessary for the magnetic field in the core to change in order to induce the voltage in the secondary winding.
The secondary voltage may be larger, smaller, or equal to the primary voltage; it depends on the ratio of the number of turns in the secondary winding to the number of turns in the primary winding. In some cases, there may be more than one secondary. The number of turns in a given secondary divided by the number of turns in the primary is called the turns ratio, given by the following equation:
\[n={{N}_{sec}}/{{N}_{pri}}\]
Where
n is turns ratio
Nsec is number of turns in the secondary winding
Npri is number of turns in the primary winding
When the transformer has a larger number of turns in the secondary winding than it has in the primary winding, the output voltage is greater than the input voltage; this transformer is a step-up transformer. The turns ratio will be greater than 1. When the transformer has a smaller number of turns in the secondary winding than it has in the primary winding, the output voltage is smaller than the input voltage; this transformer is a step-down transformer. The turns ratio will be less than 1. Although the idea of the turns ratio is useful to understand how a transformer operates, most transformers are marked by the required input (primary) voltage and the corresponding output (secondary) voltage rather than the turns ratio. The ratio of output voltage to input voltage also equals the turns ratio:
\[n={{V}_{sec}}/{{V}_{pri}}\]
EXAMPLE 1
What is the turns ratio of a transformer that has a primary voltage of 120 V and a secondary voltage of 24 V?
Solution
\[n=\frac{{{V}_{sec}}}{{{V}_{pri}}}=\frac{24V}{120V}=0.2\]
The turns ratio is less than 1, which is always the case when the output voltage is less than the input voltage for electronic power transformers.
Transformers range in size from the thumbnail-size coupling transformers used in electronics to huge units weighing hundreds of tons that are used to interconnect portions of power grids. Transformers are found in nearly all electronic devices using utility voltage and are essential for high-voltage power transmission. Two basic types of transformers are used in power applications: single-phase and three-phase. Most residential applications are single-phase; three-phase is used in many industrial applications.
Review Questions
- What is a capacitor? What is the unit of capacitance?
- How does a capacitor store energy?
- What is an inductor?
- What happens when the current changes in an inductor?
- What is the unit of inductance?
- What is Lenz’s law?
- What is impedance?
Answers
- A capacitor is a component with the ability to store charge. The unit of capacitance is the Farad.
- Capacitors store energy in the electric field between the plates.
- An inductor is an insulated coil of wire that has a magnetic field when current is in it.
- Changing current induces a voltage across the inductor.
- The Henry
- A changing current in a coil induces a voltage that opposes the change in the current.
- Impedance is total opposition to ac from the combination of resistance and reactance.