Electric Machine Losses
Mechanical Losses
Mechanical losses result when any electric machine operates. It is simply not possible to make a machine 100 per cent efficient. In electric machines the losses are minimal, however, and electric machines may approach 98 per cent efficiency.
The normal losses in a rotating electric machine are friction and windage. Friction results from surfaces rubbing together and there are few surfaces in contact in an electric motor. The rotor runs on the bearings and is free to spin inside the stator, so the only friction losses will be the bearings rubbing against their grease, seals and bearing caps. Therefore the friction losses in a motor are minimal.
Windage results from the rotating parts driving air around the motor, inside or out. Fans inside a motor increase the windage but help to dissipate heat, so it is a working loss; a loss we are happy to accept because it does a job.
The only other mechanical loss, as far as the motor is concerned, is load. Although the whole purpose of an electric motor is to provide mechanical energy, from an electrical point of view, mechanical load is also a loss.
Electrical Losses
Electrical losses in a motor can be grouped under two main areas. These are magnetic losses and resistive losses. Magnetic losses are due to eddy current and hysteresis losses in the magnetic fields of the stator and rotor. The eddy current losses can be reduced by using laminated windings, while the hysteresis losses can be reduced by using special steel such as ‘transformer steel’ for the laminations.
The resistive losses are due to the heating effect of an electric current. The value of the resistive losses can be determined using Joule’s law H = I2Rt. It can be seen from the formula that the higher the resistance of the windings, the greater the resistance losses. It can also be seen that the heat produced by an electric current is proportional to the current squared.
Both the magnetic and resistance losses appear in the motor as heat. Figures 1 and 2 show the energy losses in a generator and a motor.
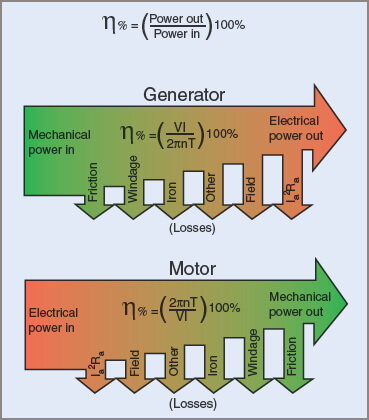
Figure 1 Energy flow and losses in Electric Generator and Motor

Figure 2 Electric Motor/generator losses
Mechanical Power
Mechanical power is the power out, which is calculated using the formula P = 2πnT; where 2π is the conversion factor between linear and rotational speed, n is the speed in revolutions per second, and T is the torque at the shaft in newton meters (Nm). As the speed of motors is normally given in revolutions per minute, the equation becomes P = 2πnT/60.
Motors are designated by their shaft output power. Many older motors are rated in horsepower (HP). To convert to watts, 1 HP = 746 W. Also, older motors may also have a torque given in foot-pounds or ftlbs—1ftlb = 1.35582 Nm (∼ 1.36).
Example 1
A 400 V, three-phase, 50 Hz, four-pole induction motor has a full load speed of 1440 rpm.
Calculate the power produced by the motor if it develops a torque of 75 Nm.

Example 2
If the three-phase motor in Example 1 has an input power of 12.6 kW, determine the losses in the motor at this load.
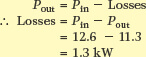
Electrical Power
Electrical power is calculated using the formula P = VI for DC; P = VIcosΦ for AC single phase; and √3VIcosΦ for three phase.
The electric power requirement of a motor is always greater than the nominated mechanical power derived from the motor.
Example 3
Determine the input power of a 400 V, three-phase motor that draws 40 A at a power factor of 0.9 lagging.

Example 4
Determine the input power of a 230 V, single-phase motor that draws 5.2 A at a power factor of 0.86 lagging.

Example 5
Determine the input power of a 220 V, DC motor with a load current of 40 A.
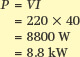
Electric Machine Efficiency
The efficiency of any electric machine is calculated from its input energy and output energy. The normal way to describe the efficiency is by percentage of output power over input power, so the calculation is:
![]()
Example 6
A 0.75 kW, 230 V, single-phase motor has an input power 1 kW at full load.
Determine the percentage efficiency of the motor at this load.
![]()
Example 7
A motor running at 1425 rpm produces a torque of 30 Nm.
If the input power at this torque is 5.3 kW, determine the percentage efficiency at this load.

Example 8
A 400 V, two-pole, three-phase motor draws 14.4 A at full load, with a power factor of 0.84.
If the motor is 86% efficient and is running at 2890 rpm, how much torque can be continuously drawn from this motor?


