Magnetization Curve Explanation

Magnetization Curve Definition

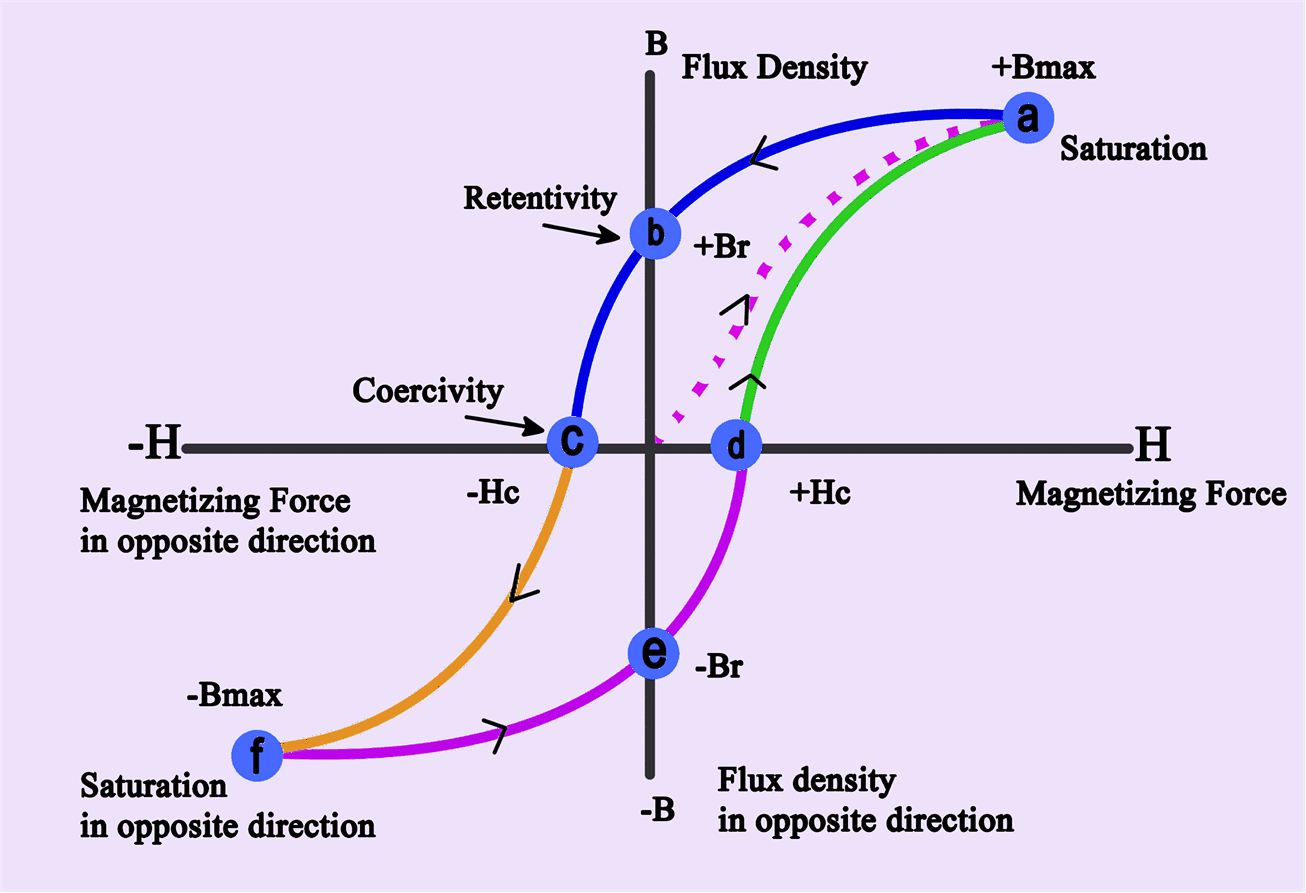
A curve, or loop, plotted on B-H coordinates showing how the magnetization of a ferromagnetic material varies when subjected to a periodically reversing magnetic field, is known as Hysteresis Loop or Magnetization Curve.

Non-Magnetic Materials

The reluctance of non-magnetic materials is not affected by the density of flux in those materials. Flux (Φ) therefore will vary directly with the m.m.f. (IN), and flux density (B) will consequently vary directly with the magnetizing force H.

For non-magnetic materials, B varies directly with H and therefore the graph of B against H will be a straight line.

Magnetic Materials

When values of B are plotted against values of H for a magnetic material, the resulting graph is in the form of a curve. Table 1 shows figures for an iron sample.

Table 1 Magnetization Curve for a Magnetic Material

Magnetizing force H (At/m)	Flux density B (Wb/m2)	Permeability μ= B/H	Relative permeability μr = μ/μo
100	0.04	0.00040	318
200	0.12	0.00060	477
300	0.40	0.00130	1058
400	0.90	0.00225	1790
500	1.00	0.00225	1591
600	1.06	0.0017	1408
700	1.11	0.00159	1265
800	1.15	0.00144	1146
900	1.18	0.00131	1042
1000	1.21	0.00121	963
1200	1.25	0.00104	828
1400	1.29	0.00092	732
1600	1.32	0.00083	660
2000	1.36	0.00068	541

A graph plotted from these figures is shown in Figure 1. Since values of B are plotted against values of H, the graph is known as a B/H curve or magnetization curve. These curves are commonly used as a means of comparing the magnetic characteristics of different types of magnetic materials.

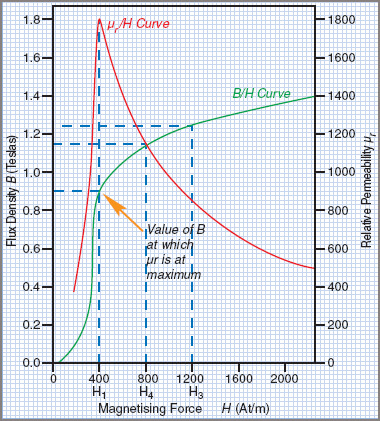
Figure 1 Flux – magnetization curve

Magnetic Saturation

Reference to the B/H curve in Figure 1 shows that, when the value of H is low, small increases in the value of the magnetizing force (H) will produce large increases in the value of the flux density (B). This is shown by the section of the curve that slopes steeply.

For higher values of H and B, it can be seen that increases in H will produce progressively smaller increases in B. Further increases of H to the value H3 will result in an even smaller increase in B from B2 to B3. As the magnetization increases towards 2000 AT/m, the flux density increases less and less. This indicates that magnetic saturation is taking place.

Saturation is said to occur at a flux density near the center of the ‘knee’ of the B/H curve. In practice, it is not economical to magnetize steel to a flux density much beyond the point of magnetic saturation. A large increase in magnetizing current produces only a small increase in flux density, resulting in a waste of electrical power, without achieving any useful increase in flux.

The permeability of ferromagnetic materials changes with differing values of flux density. For a given flux density, permeability (μ) is equal to the ratio B/H, which may be proved by applying the basic magnetic equation in the following manner:

Table 1 gives typical values of B and H for iron. Therefore it is possible to calculate permeability for each particular flux density and magnetizing force. In Table 1 columns 3 and 4, values for μ and μ_r have been calculated from the given values of B and H.

The values of μ_r have been plotted against the values of H in Figure 1 to give the μ_r/H curve. The graph shows that the permeability curve rises steeply to a peak. Beyond this point of maximum permeability, the curve slopes away quite rapidly. This indicates that permeability becomes progressively less as H is increased beyond the value that causes magnetic saturation.

Comparison of B/H Magnetization Curves

Figure 2 illustrates the magnetization curves for silicon steel, cast steel and cast iron.

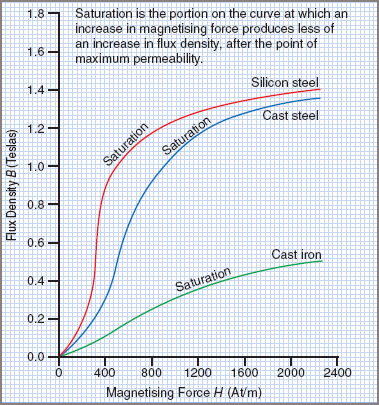
Figure 2 Magnetization Curves

The following points should be noted:

1.	The materials tend to become magnetically saturated in the region that corresponds with the centers of the ‘knees’of the respective curves.
2.	When the value of H is in the lower ranges, much greater flux density will be produced in silicon steel compared with cast steel or cast iron.
3.	Silicon steel saturates at a slightly lower value of flux density than cast steel.
4.	Cast iron saturates at much lower values of flux density than either silicon steel or cast steel. It is also much harder to magnetize than either of the above materials.