Practical op-amps are not ideal but exhibit limitations that should be considered in the design of instrumentation. In particular, in dealing with relatively large voltages and currents, and in the presence of high-frequency signals, it is important to be aware of the non-ideal properties of the op-amp.
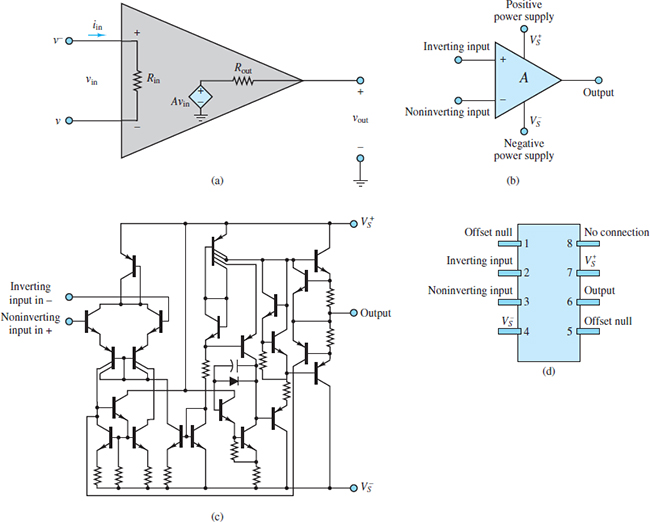
Figure a: Operational Amplifier
Voltage Supply Limits
As indicated in Figure a, operational amplifiers (and all amplifiers, in general) are powered by external DC voltage supplies VS+ and VS–, which are usually symmetric and on the order of ±10 to ±20 V. Some op-amps are especially designed to operate from a single voltage supply, but for the sake of simplicity from here on we shall consider only symmetric supplies.
The effect of limiting supply voltages is that amplifiers are capable of amplifying signals only within the range of their supply voltages; it would be physically impossible for an amplifier to generate a voltage greater than VS+ or less than VS–. This limitation may be stated as follows:
\[{{V}_{S}}^{-}<{{v}_{0}}<{{V}_{S}}^{+}\begin{matrix}{} & {} & (1) \\\end{matrix}\]
For most op-amps, the limit is actually approximately 1.5 V less than the supply voltages. How does this practically affect the performance of an amplifier circuit? An example will best illustrate the idea.
Note how the voltage supply limit actually causes the peaks of the sine wave to be clipped in an abrupt fashion. This type of hard nonlinearity changes the characteristics of the signal quite radically and could lead to significant errors if not taken into account.
Just to give an intuitive idea of how such clipping can affect a signal, have you ever wondered why rock guitar has a characteristic sound that is very different from the sound of classical or jazz guitar? The reason is that the “rock sound” is obtained by over-amplifying the signal, attempting to exceed the voltage supply limits, and causing clipping similar in quality to the distortion introduced by voltage supply limits in an op-amp. This clipping broadens the spectral content of each tone and causes the sound to be distorted.
One of the circuits most directly affected by supply voltage limitations is the op-amp integrator.
Frequency Response Limits
Another property of all amplifiers that may pose severe limitations to the op-amp is their finite bandwidth. We have so far assumed, in our ideal op-amp model, that the open-loop gain is a very large constant. In reality, A is a function of frequency and is characterized by a low-pass response. For a typical op-amp,
\[A(j\omega )=\frac{{{A}_{0}}}{1+j\omega /{{\omega }_{0}}}\begin{matrix}{} & Finite\text{ }bandwidth\text{ }limitation & (2) \\\end{matrix}\]
The cutoff frequency of the op-amp open-loop gain ω0 represents approximately the point where the amplifier response starts to drop off as a function of frequency and is analogous to the cutoff frequencies of the RC and RL circuits.
Figure 1 depicts A (jω) in both linear and decibel plots for the fairly typical values A0 = 106 and ω0 = 10π. It should be apparent from Figure 1 that the assumption of a very large open-loop gain becomes less and less accurate for increasing frequency. Recall the initial derivation of the closed-loop gain for the inverting amplifier: In obtaining the final result Vo/VS = −RF/RS, it was assumed that A → ∞. This assumption is clearly inadequate at the higher frequencies.

Figure 1 Open-loop gain of practical op-amp (a) amplitude ratio response; (b) dB response
The finite bandwidth of the practical op-amp results in a fixed gain-bandwidth product for any given amplifier. The effect of a constant gain-bandwidth product is that as the closed-loop gain of the amplifier is increased, its 3-dB bandwidth is proportionally reduced until, in the limit, if the amplifier were used in the open-loop mode, its gain would be equal to A0 and its 3-dB bandwidth would be equal to ω0. The constant gain-bandwidth product is therefore equal to the product of the open-loop gain and the open-loop bandwidth of the amplifier: A0ω0 = K.
When the amplifier is connected in a closed-loop configuration (e.g., as an inverting amplifier), its gain is typically much less than the open-loop gain and the 3-dB bandwidth of the amplifier is proportionally increased. To explain this further, Figure 2 depicts the case in which two different linear amplifiers (achieved through any two different negative feedback configurations) have been designed for the same op-amp. The first has closed-loop gain G1 = A1, and the second has closed-loop gain G2 = A2.
The bold line in the figure indicates the open-loop frequency response, with gain A0 and cutoff frequency ω0. As the gain decreases from A0 to A1, the cutoff frequency increases from ω0 to ω1. As the gain decreases to A2, the bandwidth increases to ω2. Thus:
The gain-bandwidth product of any given op-amp is constant.
\[{{A}_{0}}\times {{\omega }_{0}}={{A}_{1}}\times {{\omega }_{1}}={{A}_{2}}\times {{\omega }_{2}}=K\begin{matrix}{} & {} & (3) \\\end{matrix}\]
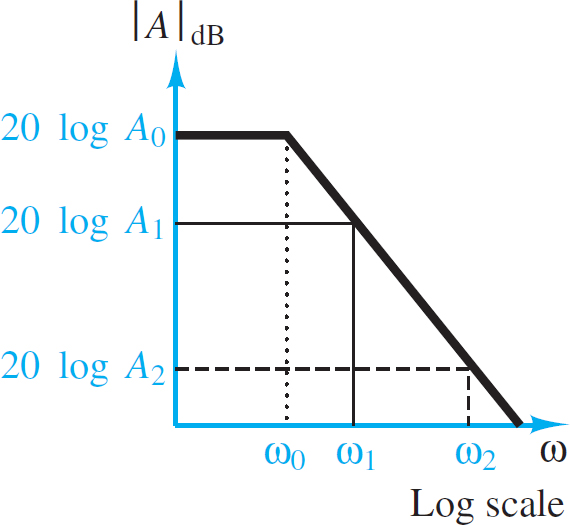
Figure 2
Input Offset Voltage
Another limitation of practical op-amps results because even in the absence of any external inputs, it is possible that an offset voltage will be present at the input of an op-amp. This voltage is usually denoted by ±Vos, and it is caused by mismatches in the internal circuitry of the op-amp.
The offset voltage appears as a differential input voltage between the inverting and non-inverting input terminals. The presence of an additional input voltage will cause a DC bias error in the amplifier output.
Typical and maximum values of Vos are quoted in manufacturers’ data sheets. The worst-case effects due to the presence of offset voltages can therefore be predicted for any given application.
Input Bias Currents
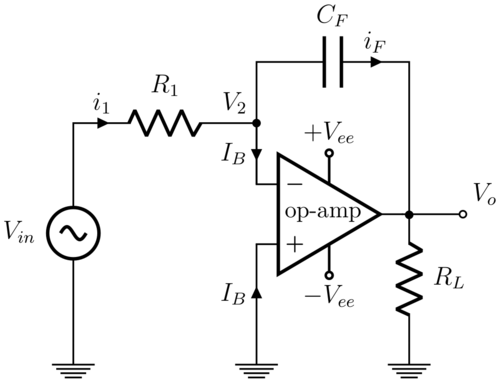
Another non-ideal characteristic of op-amps results from the presence of small input bias currents at the inverting and non-inverting terminals. Once again, these are due to the internal construction of the input stage of an operational amplifier. Figure 3 illustrates the presence of nonzero input bias currents IB going into an op-amp.

Figure 3
Typical values of IB+ and IB– depend on the semiconductor technology employed in the construction of the op-amp. Op-amps with bipolar transistor input stages may see input bias currents as large as 1 μA, while for FET input devices, the input bias currents are less than 1 nA. These currents depend on the internal design of the op-amp and are not necessarily equal.
\[{{I}_{OS}}={{I}_{B+}}-{{I}_{B-}}\begin{matrix}{} & {} & (4) \\\end{matrix}\]
The latter parameter is sometimes more convenient from the standpoint of analysis.
Output Offset Adjustment
Both the offset voltage and the input offset current contribute to an output offset voltage Vo, os. Some op-amps provide a means for minimizing Vo, os. For example, the μA741 op-amp provides a connection for this procedure.
Figure 4 shows a typical pin configuration for an op-amp in an eight-pin dual-in-line package (DIP) and the circuit used for nulling the output offset voltage. The variable resistor is adjusted until vout reaches a minimum (ideally, 0 V). Nulling the output voltage in this manner removes the effect of both input offset voltage and current on the output.
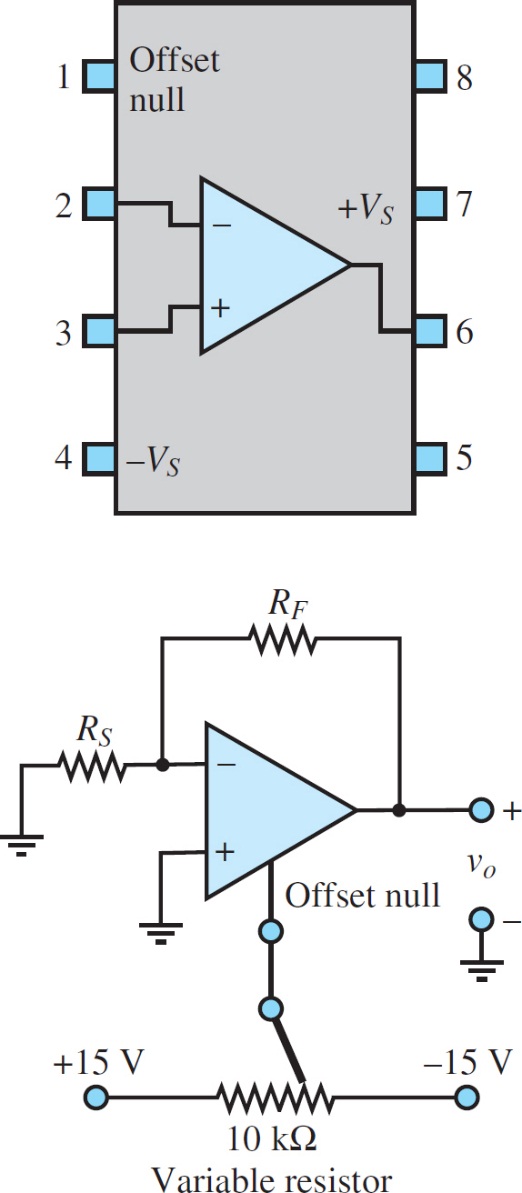
Figure 4 Output offset voltage adjustment
Slew Rate Limit
Another important restriction in the performance of a practical op-amp is associated with rapid changes in voltage. The op-amp can produce only a finite rate of change at its output. This limit rate is called the slew rate.
Consider an ideal step input, where at t = 0 the input voltage is switched from 0 to V volts. Then we would expect the output to switch from 0 to AV volts, where A is the amplifier gain. However, vo can change at only a finite rate; thus,
\[{{\left| \frac{d{{v}_{0}}}{{{d}_{t}}} \right|}_{\max }}={{S}_{0}}\begin{matrix}{} & Slew\text{ }rate\text{ }limitation & (5) \\\end{matrix}\]
Figure 5 shows the response of an op-amp to an ideal step change in input voltage. Here, S0, the slope of vo, represents the slew rate.
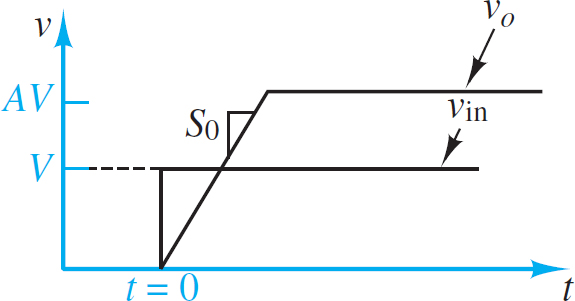
Figure 5 Slew rate limit in op-amps
The slew rate limitation can affect sinusoidal signals, as well as signals that display abrupt changes, as does the step voltage of Figure 6. This may not be obvious until we examine the sinusoidal response more closely.
It should be apparent that the maximum rate of change for a sinusoid occurs at the zero crossing, as shown by Figure 7. To evaluate the slope of the waveform at the zero crossing, let
\[\begin{matrix}{{v}_{in}}(t)=V\sin \omega t & such\text{ }that & {{v}_{0}}(t)=AV\sin \omega t & (6) \\\end{matrix}\]
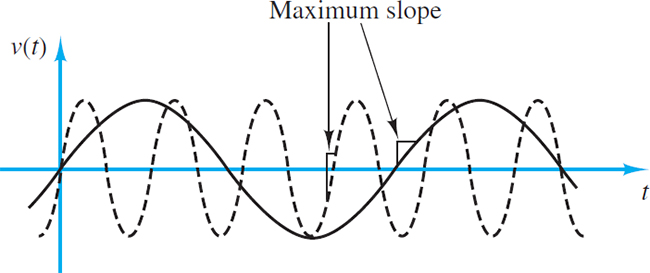
Figure 7 The maximum slope of a sinusoidal signal varies with the signal frequency.
Then:
\[\frac{d{{v}_{0}}}{dt}=\omega AV\cos \omega t\begin{matrix}{} & {} & (7) \\\end{matrix}\]
The maximum slope of the sinusoidal signal will therefore occur at ωt = 0, π, 2π, . . ., so that
\[{{\left| \frac{d{{v}_{0}}}{{{d}_{t}}} \right|}_{\max }}=\omega AV={{S}_{0}}\begin{matrix}{} & {} & (8) \\\end{matrix}\]
Thus, the maximum slope of a sinusoid is proportional to both the signal frequency and the amplitude. The curve shown by a dashed line in Figure 7 should indicate that as ω increases, so does the slope of v(t) at the zero crossings. What is the direct consequence of this result, then?
Short-Circuit Output Current
Recall the model for the op-amp shown in Figure 3, which depicted the internal circuit of the op-amp as an equivalent input impedance Rin and a controlled voltage source Avin.
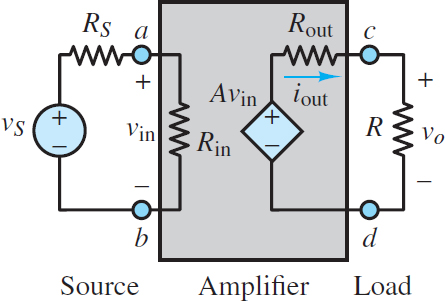
Figure 7a: Simple voltage amplifier model
In practice, the internal source is not ideal because it cannot provide an infinite amount of current (to the load, to the feedback connection, or to both). The immediate consequence of this non-ideal op-amp characteristic is that the maximum output current of the amplifier is limited by the so-called short-circuit output current ISC:
\[\left| {{i}_{out}} \right|<{{I}_{SC}}\begin{matrix}{} & Short-circuit\text{ }output\text{ }current\text{ }limitation & (9) \\\end{matrix}\]
To further explain this point, consider that the op-amp needs to provide current to the feedback path (in order to “zero” the voltage differential at the input) and to whatever load resistance, Ro, may be connected to the output. Figure 8 illustrates this idea for the case of an inverting amplifier, where ISC is the load current that would be provided to a short-circuit load (Ro = 0).
Figure 8
Common-Mode Rejection Ratio (CMRR)
The CMRR is an amplifier characteristic that can be found in the data sheet for any particular amplifier, such as a 741 operational amplifier.
$\begin{matrix}CMMR=20\log \left| \frac{{{A}_{DM}}}{{{A}_{CM}}} \right| & {} & in\text{ }dB \\\end{matrix}$