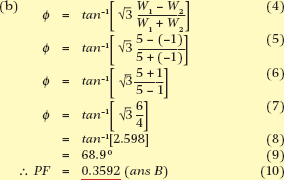Different methods are utilized in order to measure three-phase power in a three-phase circuit. In this article, we are going to discuss the following methods in detail:
- One Wattmeter Method (4-Wire System)
- One Wattmeter Method (3-Wire System)
- Two Wattmeters Method (3-Wire System)
- Three Wattmeters Method (3-Wire System)
- Three Wattmeters Method (4-Wire System)
- Electronic Three-Phase Power Meter
One Wattmeter (4-Wire System)
The single wattmeter is connected between one line and neutral in a three-phase, 4-wire system (see Figure 1). The total power drawn from a three-phase supply is found by adding the separate values of power consumed by each phase.
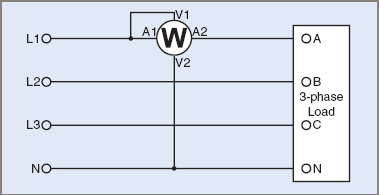
Figure 1 One Wattmeter 4-Wire
In the case of a balanced load (an equal load and power factor on each phase): Ptotal = 3PA = 3PB = 3PC = 3 times the wattmeter reading in any of the three lines
For an unbalanced load, the wattmeter has to be connected or switched into each phase in turn and the individual power readings added:
${{P}_{total}}={{P}_{A}}+{{P}_{B}}+{{P}_{C}}$
Advantages
| 1. | One wattmeter only is required. |
| 2. | It is suitable for both balanced and unbalanced loads. |
Disadvantages
| 1. | A neutral connection is required for the wattmeter |
| 2. | It is not accurate for unbalanced fluctuating loads. |
| 3. | The wattmeter has to be connected or switched into each phase in turn for unbalanced loads. The switch must not break the line when switching. |
One Wattmeter (3-Wire System)
With a 3-wire system, no neutral is available and, because there is a 30º phase shift between line and phase voltages, it is necessary to provide an artificial star point so that the correct voltage at the correct phase angle is applied to the wattmeter.
Two impedances, each matching the impedance of the voltage circuit in the wattmeter, must be connected in star with the meter voltage circuit (Figure 2) and to the other two lines. Resistors matching the resistance of the voltmeter circuit must be very close approximations for this purpose.

Figure 2 One Wattmeter 3-Wire
For balanced loads only:
${{P}_{total}}=3{{P}_{A}}=3\text{ }times\text{ }wattmeter\text{ }reading$
For balanced and unbalanced loads:
${{P}_{total}}={{P}_{A}}+{{P}_{B}}+{{P}_{C}}$
Advantages
| 1. | One wattmeter only is required. |
| 2. | It is suitable for both balanced and unbalanced loads. |
Disadvantages
| 1. | Two matching impedances are required to provide an artificial neutral. |
| 2. | It is not accurate for unbalanced fluctuating loads. |
| 3. | The wattmeter has to be connected or switched into each phase in turn for unbalanced loads. The switch must not break the line when switching. |
Two Wattmeters (3-Wire System)
A method for measuring the power consumed in a three-phase, 3-wire circuit is shown in Figure 3. The two meters have their current windings in any two lines and both voltage windings are connected to the third line. Neither meter alone indicates the total power in the circuit, but the two meters together, by their algebraic sum, indicate the power consumed, that is:
${{P}_{total}}={{W}_{1}}+{{W}_{2}}$
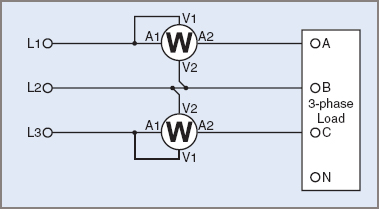
Figure 3 Two Wattmeter 3-Wire
For a balanced load with unity power factor, both meter readings will be equal. For all other conditions, the meters will show different readings.
If the lower-value meter indication is W1 and the higher one W2, then, as the power factor decreases, W1 registers less and less of the total power. When the power factor is 0.5 with a balanced load, W1 will read zero and W2 will read the total power. Should the power factor fall further (to, say, 0.3), W1 will read even less (i.e. W1 will attempt to read a negative value of power consumption). If the current or voltage connections to the meter are reversed, the numerical value of W1 can be obtained, but it must be noted that it is a negative value. The total power in this case is still the algebraic sum of W1and W2. That is:
${{P}_{total}}=\left( -{{W}_{1}}+{{W}_{2}} \right)={{W}_{2}}-{{W}_{1}}$
Should the power be reduced to zero with a balanced load (pure capacitance or inductance), W1 would read a negative value numerically equal to W2 and the algebraic sum would be zero:
${{P}_{total}}={{W}_{2}}-{{W}_{1}}=0$
This also agrees with the concept of a purely reactive circuit.
The two-wattmeter method may be used on three-phase, 3-wire systems to obtain load power values whether the load is balanced or unbalanced, or star- or delta-connected, but it cannot be used on a 4-wire, star-connected system because a single-phase component of current might be flowing in the line (and neutral) having no wattmeter current-coil connection, and the power being consumed would not be recorded.
Only when the three-phase load is balanced is it possible to find the power factor of the load from the wattmeter readings. The tangent of the angle of lag or lead is found from:
\[\tan \varphi =\sqrt{3}\times \frac{{{W}_{1}}-{{W}_{2}}}{{{W}_{1}}+{{W}_{2}}}\]
The angle φ is obtained from tan–1 φ, and the cosine of this angle gives the power factor of the load.
Example 1
When connected to a three-phase motor, two wattmeters gave readings of 5 kW and 1 kW.
Find:
| (a) | the total power being consumed.
|
| (b) | the power factor of the motor.
|
Advantages
| 1. | Only two wattmeters are required. |
| 2. | It is useful for both balanced and unbalanced three phase, 3-wire loads. |
| 3. | The power factor can be obtained for balanced loads. |
| 4. | No neutral connection is required. |
Disadvantages
| 1. | It is suitable only for three-phase, 3-wire loads. |
| 2. | Care must be used in determining the polarity of W1. |
| 3. | The power factor cannot be obtained for unbalanced loads. |
| 4. | It is not suitable for power or power factor readings with three-phase, 4-wire systems. |
Three Wattmeters (3-Wire System)
With a 3-wire system, no neutral is available, so an artificial neutral must be provided. However, if identical wattmeters are used, the three voltage circuits can be connected to provide a star point, as shown in Figure 4:
${{P}_{total}}={{W}_{1}}+{{W}_{2}}+{{W}_{3}}$
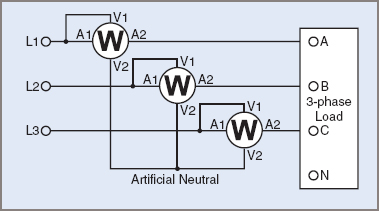
Figure 4 Three Wattmeter 3-Wire
Advantages
| 1. | It is suitable for both balanced and unbalanced loads. |
| 2. | It is convenient for obtaining total power. |
| 3. | It is more accurate than one wattmeter for fluctuating loads. |
Disadvantage
Three wattmeters are needed.
Three Wattmeters (4-Wire System)
The three-phase, 4-wire system is basically three separate supplies with only a common neutral. The total power is obtained by connecting three wattmeters, as shown in Figure 5:
${{P}_{total}}={{W}_{1}}+{{W}_{2}}+{{W}_{3}}$
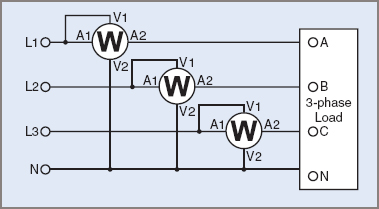
Figure 5 Three Wattmeter 4-Wire
Advantages
| 1. | It is suitable for both balanced and unbalanced loads. |
| 2. | It is convenient for obtaining total power. |
| 3. | It is more accurate than one wattmeter for fluctuating loads. |
Disadvantage
Three wattmeters are needed.
Electronic Three-Phase Power Meter
A typical electronic power meter measures all three line voltages, and neutral if a 4-wire system, and three line currents through Current Transformers (CTs) when higher power levels are measured (see Figures 6 and 7).
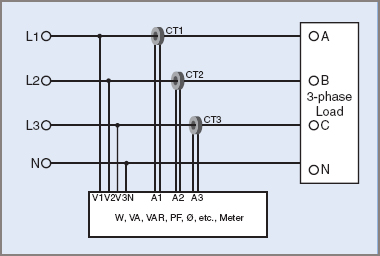
Figure 6 Electronic Three-Phase Power Meter

Figure 7 Panel Power Meter
Total power is measured by linear electronics in some instruments using operational amplifiers to calculate power continuously before displaying on an analogue meter or digital readout.
Digital instruments may use analogue-to-digital converters to measure voltage and current, and zero-crossing comparators to measure phase angle. From those values, digital electronics are used to calculate power, reactive and apparent power, Power Factor and phase angle.
The most recent instruments use computer technology to improve on digital instruments, providing greater accuracy, more functions and features such as frequency, Total Harmonic Distortion (THD), crest factor, true RMS measurement and may even display the waveforms or phasors. Figure 8 shows a technician using a power-analyzing instrument.

Figure 8 Fluke Power Analyzer in Use
Advantages
| 1. | It suits any type of load or system, 3- or 4-wire. |
| 2. | It can measure V, I, W, VA, VAR, PF, Ø, F, THD etc. |
| 3. | No calculations are required. |
| 4. | Some units show waveforms and/or phasors. |
| 5. | It has robust construction. |
| 6. | It offers good environmental protection, often IP56 or better. |
| 7. | Once set up, measurements are selected by push button. |
Disadvantage
| 1. | It may require a battery! |