Similar to other types of electric machines, a three-phase induction machine can work as a generator and as a motor. For this machine, however, because the stator must be connected to the three-phase circuit, the difference between being a motor or functioning as a generator lies in the speed of the rotor.
In general, if the rotor speed is higher than the synchronous speed, then it behaves as a generator, and if the rotor speed is less than the synchronous speed, it becomes a motor.
The synchronous speed is determined by the line frequency and the number of poles of the stator winding.
The developed rotating magnetic field, after the stator is electrically connected, revolves at the synchronous speed. This causes the rotor to follow the rotating magnetic field and rotate (thus, a motor), but, if the rotor shaft is given mechanical energy to rotate faster than the speed of the magnetic field, then the machine behaves as a generator.
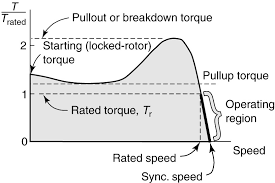
Figure 1 shows a typical characteristic curve of an induction machine. It involves torque and speed relationships.
The curve consists of two almost symmetrical curves, one representing the induction motor operation and one associated with the generator operation. This curve can be shown differently (swapping the coordinates) or can be continued from motor side for other characteristics (such as dynamic braking, where the direction of the developed torque is to the opposite of rotation, thus, a braking action), but here we are only interested in the following information that can be observed from the curve:
Figure 1 Torque-speed characteristic curve of a three-phase induction motor & generator
- If the rotor speed is less than the synchronous speed (NS), the machine acts as a motor; it delivers torque to a load. The number of torque changes based on a given speed of the load.
- The only part of the curve, which is almost linear, is good for operation. For both functions, as a motor and as a generator, outside of this linear segment is not suitable for operating the machine.
- As a motor, the machine has a starting torque (at zero speed); thus, the machine is a self-starter.
- In the linear (operating) region as a motor, as torque increases, the speed decreases, and vice versa. At the synchronous speed NS, no torque can be delivered by the motor.
- Within the linear region as a generator, if speed is increased, torque demand also increases, and vice versa. This is a self-regulatory behavior; it prevents a machine from going into a runaway state.
- If the machine runs at a speed equal to NS, it does not produce any power (because the torque is zero at this point, and power = torque × speed).
The above observations imply that as a motor the speed is always less than the synchronous speed, and as a generator, the machine must always be run above the synchronous speed.
Except in a particular mode, many wind turbines used an induction generator. This is an intelligent choice because the variable wind speed can move the operating point of an induction generator along the linear portion of the generator characteristic curve. In this way, with higher wind speeds a generator turns faster and produces more power without affecting the synchronous speed.
The curve depicted in Figure 1 has a typical shape. The exact form of the curve depends on the physical properties of each individual machine, including the resistance in the windings and the external circuit for a WRIM.
The difference between the speed of the rotating magnetic field (the synchronous speed) and the rotor speed is called the slip speed, and the ratio of this difference to the synchronous speed is called slip.
The magnitude of slip, expressed in percentage, is usually small, say below 3 percent. It can be determined from
Slip speed: Difference between the speeds of the rotor and the rotating magnetic field in an AC induction machine.
Slip: The fact that the rotor of an induction machine does not rotate with the same speed as the rotating magnetic field (turning faster in a generator and slower in a motor).
\[\begin{matrix} S=\frac{{{N}_{s}}-N}{{{N}_{s}}}=1-\frac{N}{{{N}_{s}}} & {} & \left( 1 \right) \\\end{matrix}\]
Where NS is the synchronous speed and N is the rotor speed. For a generator NS < N and, thus, S becomes negative. Note, that as a generator, no matter how much N is larger than NS the frequency of the electricity injected into the AC line is NS.
The rotational speed N of an induction motor, and thus the slip, depends on the operating point, which depends on a load torque requirement (so, for a motor, if torque is higher, speed is lower). The same is true for a generator; an equilibrium point is reached when the torque demand on the shaft is fulfilled by the generator prime mover.
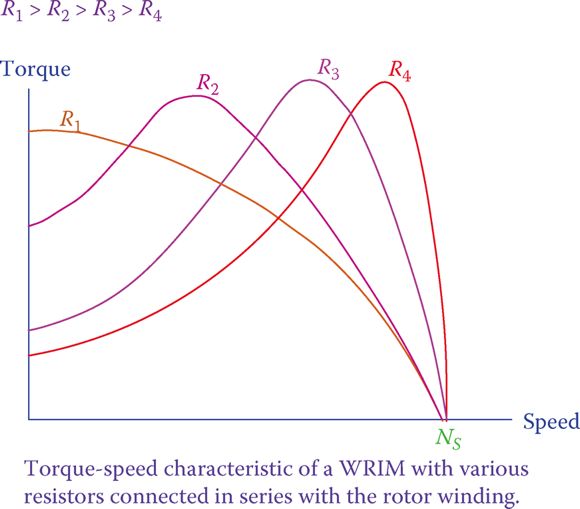
Figure 2 Change in the form of the torque-speed curve of induction motor due to external resistance.
In a wound rotor induction machine, the external resistor R can be modified. This alters the characteristic curve of a machine (both as a generator and as a motor). Figure 2 illustrates the effect of this change (only the motor part is shown). The effect is in slip and torque at zero speed.
In a squirrel cage machine, there is no external resistor. However, the same effect (change in the characteristic curve) can be obtained by altering the shape (not being round) and position (nearer or farther from the center) of the bars of the cage. Sometimes two sets of bars are used, and it is called the double-cage machine.
In a three-phase induction motor, there are three connections to be made. If (any) two connections are interchanged, the direction of rotation reverses.