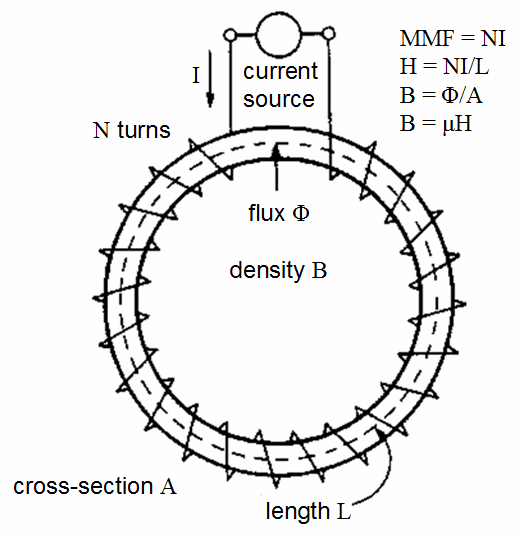
The m.m.f. required to magnetize a unit length of a magnetic path is termed the magnetizing force or magnetic field intensity (H) for that portion of the magnetic circuit.
The magnetic field intensity is applicable only to that section of the magnetic circuit, made of the one material and with a constant cross-section. The unit is expressed in ampere-turns per meter and the symbol is H.
In a similar fashion to that for magnetomotive force, the ‘turns’ part of the expression is dimensionless and in pure SI units should be omitted, leaving it as amperes per meter. For all practical purposes, however, the more descriptive term is ampere-turns per meter. That is:
![]()
Where:
- l = length of magnetic circuit in meters
Note: Be sure to convert length into meters! Magnetizing force must not be confused with magnetomotive force.
Example
Find the magnetic field intensity (H) in the magnetic circuit given below:
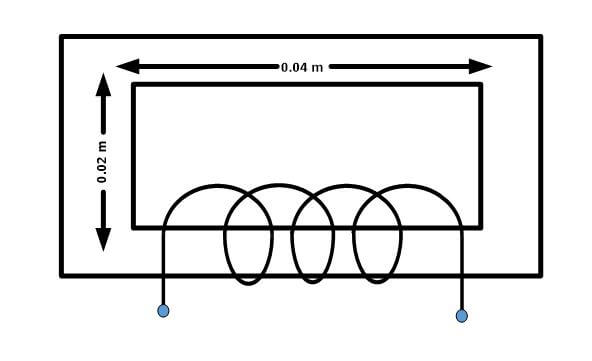
Solution:
Here, we will calculate the magnetic field intensity (H) using the following formula:
\[H=\frac{N\times I}{l}=\frac{(2.5*{{10}^{2}})*(1.5*{{10}^{-1}})}{1.2*{{10}^{-1}}}\]
\[H=\frac{3.75*{{10}^{1}}}{1.2*{{10}^{-1}}}=3.125*{{10}^{2}}A-t/m\]
If we change the dimensions of the magnetic path, the value of H would also change. For example, if we double the length of the magnetic path, we should anticipate the value of magnetic field intently (H) to decrease to one-half its original value calculated above.
If, for the above magnetic circuit, physical dimensions are, then magnetizing force (H) will be;
\[H=\frac{3.75*{{10}^{1}}}{2.4*{{10}^{-1}}}=1.5625*{{10}^{2}}A-t/m\]
So, we can clearly see that, for a given number of ampere-turns, the magnetizing force varies inversely per unit length of the total magnetic path.