It is always the electric power in an electric circuit that determines how much energy is going to a device, a system, or a place, and how much that energy costs.
A good comprehension of the relationships for electric power, unit of power measurement, and the rules that determine power is very important.
You must always bear in mind that for an electric power source (e.g., generator and battery), power rating implies the maximum power that the device can deliver.
For a consumer, (a load) power rating implies the electric power requirement by the device so that within the desired operating conditions (voltage and current) it can function with good efficiency and with minimum risk of damage.
The required electric power must be available to the device so that it functions properly. If that much power is not provided (by the source, the line, or the power supply), some shortcoming can happen that can lead to damage and failures.
Electric power: Power in the form of electricity and measured by electrical units (power is the amount of work in 1 sec).
If the current does not change but the voltage doubles, the electric power doubles, and if the voltage does not change but the current doubles, the power doubles. This relationship is
\[\begin{matrix} P=VI & {} & \left( 1 \right) \\\end{matrix}\]
Where P is in watts, V is in volts, and I is in amps.
Equation 1 clearly shows that for the electric power to be constant (this situation often occurs in practice), if the voltage decreases, then the current must increase or if the current increases, the voltage must decrease. Current increase beyond a rated value is equivalent to overload, which is not desirable.
Electric Power Calculation Example 1
Measured current in the filament of a lightbulb, when connected to a 12 V battery, is 5 A. What is the electric power consumption of the lightbulb?
Solution
Power can be directly found by the product of the voltage and the current:
$P=VI=12*5=60W$
Energy and Power
“Energy” is the potential to do work, and it can be in different forms, such as electrical energy, nuclear energy, thermal energy (heat), wind energy, and solar energy. “Work” here implies a mechanical or another type of work.
Mechanical work is, for instance, when a weight is lifted or when an engine drives a car. Mechanical work is more tangible compared to other types of work. For instance, a motor can do mechanical work, but a battery does not directly do mechanical work. However, it can run a motor that does mechanical work; thus, a battery has the potential to work. It has electrical energy.
Energy can be converted from one form to another. For instance, consider a steam turbine that can do mechanical work. That is the conversion of heat to mechanical energy. In this sense, when an electric kettle heats water, it performs work. It consumes energy and converts it to work.
Energy can be measured, like any other entity, in its appropriate unit(s). Suppose that a machine or device has energy. How much energy does it have? Energy can be measured in terms of heat units like calorie and BTU (British thermal unit), work units, or energy units.
The unit for energy is joule, and units for work can be foot-pound and newton-meter. One joule is, in fact, one newton-meter.
In conjunction with the energy, we have power. We may always ask the question: “If a machine can do a certain amount of work, how long does it take to do it?” For example, how long does it take for a kettle to boil the water in it? The answer to this question stands in power, which is also used for comparison between various energy sources.
Power is the amount of work done in 1 sec by a device that can do work. This is the measure of the strength of energy sources. For instance, a smaller motor has less power than a larger motor. That is, it can do less work than the larger motor in the same duration of time or, in doing the same work for the smaller motor, it takes more time.
Similarly, it takes more time for a smaller (less powerful) kettle to boil the same amount of water compared to a larger kettle.
Thus, electric power is determined from energy divided by time.
\[Power=\frac{Energy}{Time}\]
Electric power is normally measured in watt and kilowatt. Energy is sometimes (especially in the case of electrical energy) measured in terms of the unit of power multiplied by the unit of time; that is, watt-second and kilo-watt-hour are used as units of energy.
For almost any device, including light bulbs, the power is written on the device itself or on a nameplate. In addition, the operating voltage is always shown. For example, on a lightbulb, you may see “100 W, 120 V.” This implies that
- Operating voltage of the light bulb is 120 V. You should not connect this bulb to a voltage that is considerably higher than 120 V; whereas it is generally acceptable if you connect it to 125 V, but if you apply 180 V to this bulb, you will definitely burn it out.
- If connected to 120 V, the power consumed by the light bulb is 100 W. Moreover, if you connect it to a higher voltage, the power will be more than 100 W, and if the voltage used for the bulb is lower, then the power is lower than 100 W.
Note that physically the lightbulb does not change and it has only a filament in it with a certain resistance. The resistance of the filament when it is cold is less than when it is lighted.
Electric Power Calculation Example 2
What is the resistance of the filament in a 100 W, 120 V lightbulb?
Solution
The current in the light bulb filament can be found from Equation 1:
\[I=\frac{P}{V}=\frac{100W}{120A}=0.83A\]
From V=IR,
\[R=\frac{V}{I}=\frac{120}{0.83}=144\Omega \]
Electric Power Calculation Example 3
What is the power consumption of a 100 W, 120 V lightbulb if it is connected to 110 V?
Solution
No matter to what voltage the lightbulb is connected, its filament does not change. When the light bulb is connected to 110 V, its filament still gets hot and with good precision, we can assume that its resistance stays at 144 Ω (see Example 2).
The current due to connecting this lightbulb to 110 V is
\[I=\frac{V}{R}=\frac{110V}{144\Omega }=0.764A\]
Thus the power of lightbulb is
$P=VI=110*0.764=84W$
It can be clearly seen that if the voltage applied to a lightbulb (or any other device with the resistive element) is not the same as its rated voltage, then one cannot expect to obtain the rated electric power.
Note that if the applied voltage is much smaller than the rated value, then the lightbulb filament is not heated enough and its resistance cannot be assumed to stay the same. Its resistance becomes slightly smaller.
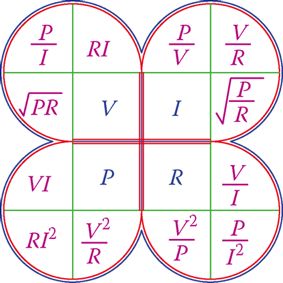
As can be seen from the Ohm’s law and from the relationship for an electric power, there are four interrelated electrical entities for any resistive load: resistance, voltage, current, and power. When any two of these values are known, the other two can be obtained.
The following equations are quite useful in obtaining the unknown quantities.
Electric Power
$\begin{align} & P={{I}^{2}}R \\ & P=\frac{{{V}^{2}}}{R} \\\end{align}$
Current
$\begin{align} & I=\frac{P}{V} \\ & I=\frac{V}{R} \\\end{align}$
Voltage
$\begin{align} & V=IR \\ & V=\frac{P}{I} \\\end{align}$
Resistance
$\begin{align} & R=\frac{V}{I} \\ & R=\frac{{{V}^{2}}}{P} \\ & R=\frac{P}{{{I}^{2}}} \\\end{align}$
All of the equations can be put together in the form of a chart shown in Figure 1.
Figure 1 Summary chart for the relationships among voltage, current, resistance, and electric power.
Measuring Electric Power and Energy
From the fact that the electric power is the product of voltage and current, it is obvious that a watt-meter to measure power must work based on a needle (if analog) or a display (if digital) whose displacement or value is proportional to the values for both the voltage and the current in a circuit.
While a watt-meter can be used in panels of electric generators to indicate the instantaneous power, it is normally not used by a technician, and it is not included in the functions of a multimeter.
However, measuring energy is very common for the calculation of electric energy cost. Each house and building is equipped with an electricity meter that measures the consumed electric energy. The basis of such a meter is a circular disk that rotates and causes a series of gears to rotate as in a clock.
The speed of rotation of this disk is proportional to the power consumed in a circuit, and the number of revolutions during a period represents the energy consumed during that period.
The unit for measuring electric power is watt.
A kilowatt (1000 watts) is a larger unit, and for even larger measures of energy production, megawatt (1,000,000 watts) is a more common unit of power.
Because energy is the product of power and time, we may write
$\begin{matrix} E=Pt & {} & \left( 2 \right) \\\end{matrix}$
If P is the electric power in watt and T is the time in second, then E determines energy in joules. It is very common in electricity that a larger unit of energy is employed.
If the power is given in kW and time in hr (3600 sec), then the unit of energy is kW-hr (kilowatt-hour). Kilowatt-hour is a unit of energy equivalent to (1000)(3600) = 3,600,000 joule.
A better understanding of kW-hr is possible in the following manner. One kW-hr is the energy consumption of one 100 W lightbulb in 10 hours, or of two 100 W lightbulbs in 5 hours, or ten 100 W lightbulbs in 1 hour.
Electric Power Calculation Example 4
A 100 W lightbulb is turned on 5 hours per day. Calculate the amount of energy consumed by the light bulb in a year.
Solution
$\begin{align} & Number\text{ }of\text{ }hours\text{ }the\text{ }light\text{ }is\text{ }on\text{ }in\text{ }a\text{ }year=365*5=1825\text{ }Hr. \\ & Energy=Pt=100*1825=182,500W-hr=182.5kW-hr \\\end{align}$
Electricity Cost Calculation Example 5
If the cost of electricity is 8 cents per kW-hr, what is the cost of electricity used by the lightbulb in Example 4?
Solution
$AnnualCost=182.5*0.08=\$14.60$
Electricity Cost Calculation Example 6
If the average daily electricity consumption in a household is 4 kW-hr during a given season, what is the monthly cost of electricity if the rate of electricity is 7.5 cents per kW-hr?
Solution
$\begin{align} & Average\text{ }Monthly\text{ }Consumption=30*4=120\text{ }kW-hr \\ & Cost=120*0.75=\text{ }\$90\\\end{align}$