A capacitor acts as a storage device to electricity. The amount of storage depends on the capacity of the capacitor. We want to study what happens if a capacitor is included with resistors connected to a DC circuit.
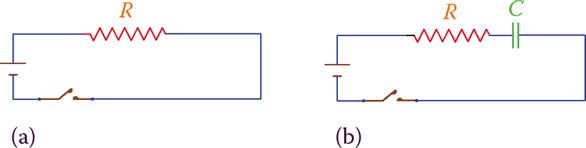
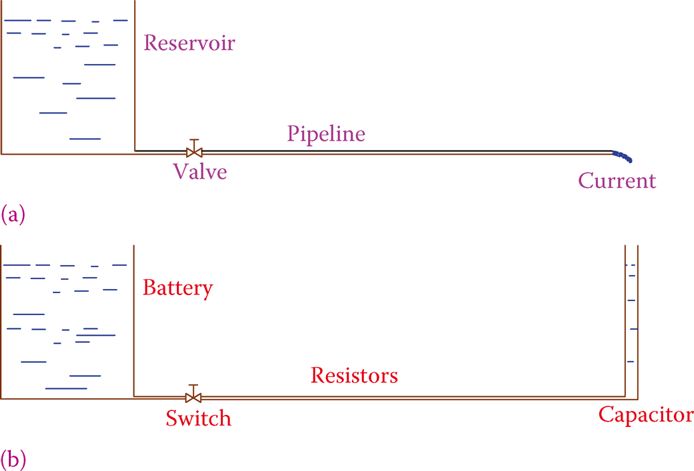
Figure 1a is a simple DC circuit with a resistive load, to which a capacitor is added, as in Figure 1b. An analogous equivalent hydraulic circuit, for better tangibility, is shown in Figure 2.
Adding a capacitor to an electric circuit is equivalent to adding a closed tank with limited capacity or a tall tank (with walls that are tall enough and comparable with the main reservoir) at the end of a pipeline.
Water flows in the pipeline in Figure 2a as the electricity flows in the circuit of Figure 1a, as long as the reservoir (battery) is not emptied.
Nevertheless, in the case of Figure 2b, a current of water flows as long as the small tank is not full. That is, for a short period of time, there is a current in the pipeline, but after a while, water stops flowing.
Moreover, this flow of water is not uniform during the period. At the beginning (when the tank is empty), more water flows but toward the end the flow of water becomes less and less, approaching zero. This is exactly what happens in the electric circuit containing a capacitor, too.
Figure 1: Adding a capacitor to a DC circuit. (a) A circuit without capacitor; normal current after the switch is closed. (b) Circuit with a capacitor; current only for a short time no current afterward.
Figure 2: Adding a small tank to the end of a pipeline. (a) Hydraulic system analogous to Figure 1a. (b) Hydraulic system analogous to the DC circuit with a capacitor, in Figure 1b.
When a capacitor is inserted inside a DC circuit, for a short period of time after the switch is turned on, current flows in the circuit. In the beginning, this current is higher but gradually becomes smaller and smaller until it diminishes. This is when the capacitor has charged, and it does not accept an electric charge anymore.
At this time and afterward, there is no current flowing in the circuit. Thus, except for a short period, in the beginning, a capacitor in a DC circuit blocks the circuit and does not allow any current.
A charged capacitor contains electricity and behaves like live electricity. It can be dangerous if the voltage is sufficiently high. The voltage level to which a capacitor charge is the same as that of the battery (power supply) if the capacitor becomes fully charged.
If the circuit is broken (the switch is turned off) while the capacitor is charging, it only partially charges and to a voltage less than the applied voltage.
A capacitor in a DC circuit blocks the current, except for only a short period following a change such as after a switch is closed (or opened if already closed).
It is interesting to know how long it takes for a capacitor to charge. In fact, in many timing devices, including electronic watches, this time period is used for timekeeping.
The time for charging or discharging a capacitor has a direct correspondence with the problem for a water tank to fill (under a given water pressure) or empty if already full (based on the height of water and the resistance of the pipeline from which water discharges).
Capacitor Charging Time
Here a simple rule is given for the calculation of the time for charging a capacitor. Referring to Figure 1b the circuit consists of a resistor with resistance R and a capacitor with capacitance C in series with each other connected to the battery (power supply) of voltage V. We define a time constant τ (the Greek letter corresponding to English t, and pronounced tow).
Time constant: Duration of time for a circuit containing a capacitor or inductor and resistors to reach 63 percent of a new value after a change has happened to the circuit (e.g., its power has been turned on or off).
$\tau =RC$
When R is defined in ohm and C in farad, τ is automatically expressed in seconds. As can be seen, the time constant τ depends on the values of R and C. It takes approximately 5× the time constant τ for the capacitor to fully charge to voltage V. This time starts from the instant that the switch is closed. But, if during this time interval the switch is opened, the capacitor does not fully charge.
The time constant is sometimes shown by T (uppercase) instead of τ.
RC Circuit Time Constant Calculation
A 51 Ω resistor and a 10 mF (milli-farad) capacitor in series are connected to a 12 V battery. How long does it take for the capacitor to charge?
Solution
The time constant is calculated first:
$\tau =RC=51*\left( {}^{10}/{}_{1000} \right)=0.51\sec $
The required time for charging the capacitor = 5τ = (5)(0.51) = 2.55 sec
Except for a very short period, in the beginning, a capacitor in a DC circuit behaves as an open circuit and does not allow any current. It takes approximately 5× the time constant for a capacitor to either charge or discharge.
Time Constant in DC Circuits
A capacitor has a storage capability for electricity. When it is part of a DC circuit, it exhibits an apparent opposition to a change in the circuit voltage.
When a switch turns on or off the power to an electric circuit, it introduces a change of voltage to the circuit. During turning the power on in a DC circuit containing a capacitor, first, the capacitor is charged. Similarly, at power off, first, a capacitor in the circuit releases its charge to the circuit. Consequently, a delay is associated with both turning on and turning off a DC circuit.
As a result of this delay, it takes a short while before the circuit containing a capacitor reaches its equilibrium and comes to its final condition when a change in voltage, either increasing or decreasing, occurs. This delay depends on the capacitance of the capacitor and the resistance in the circuit.
The delay just mentioned is approximately 5× the time constant of the circuit.
The time constant for a circuit containing capacitors with an equivalent capacitance C and resistors with an equivalent resistance R is
$\tau =RC$
When R is in ohm and C is in Farad, the time constant is determined in second.
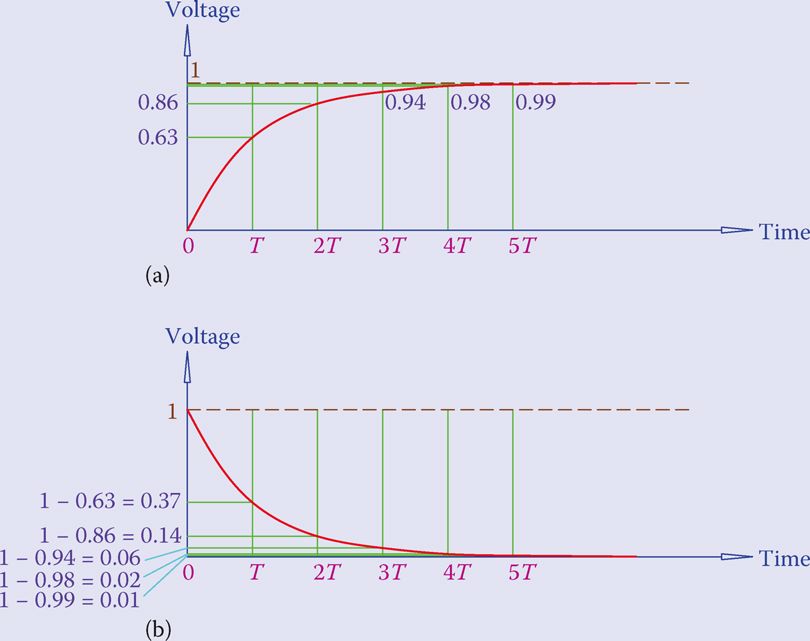
Figure 3 below shows the two cases of increasing and decreasing the voltage in a DC circuit. Because this change in voltage can be any value, it is normalized and its magnitude is shown as 1, which percentage-wise represents 100 percent.
- The figure illustrates the gradual change of voltage during the time it takes for this change. The time constant is depicted as T, and the percentage change after the elapse of each time constant T is also shown.
- For an increase in voltage (like turning on a switch), part (a) in figure 3 illustrates that subsequent to the initiation of an increase in voltage, after T seconds the voltage increases by 63 percent of the difference between the new and the old values.
- In the figure, the old value is zero, but it can be a nonzero value. After 2T sec the voltage is augmented to 86 percent of the change. After 5T, 99 percent of the change is reached, which is almost the total change to occur.
- Part (b) of figure 3 illustrates a decrease in voltage. If the change is caused by turning the power off, so that the final voltage is zero, 63 percent of the decrease in voltage takes place after one time constant. That is, the circuit voltage drops to 37 percent of its initial value.
- Accordingly, after 2T the voltage drops to 14 percent and after 5T the decrease is 99 percent and the voltage in the circuit is 1 percent of its initial magnitude. After this time the voltage change is practically zero.
Figure 3: Capacitor Charging and Discharging
The delay introduced by a capacitor has many applications, particularly in electronic circuits used in radio, TV, communications, and so on, as well as in electrical applications that need control and regulation.
By changing the time constant, through R and C, the desired delay can be obtained for any application.